loading...
Untuk lebih memahami wacana prisma, pengertian prisma, jenis-jenis prisma, unsur-unsur prisma, sifat-sifat prisma serta jaring-jaring prisma, sebaiknya anda mencoba menuntaskan soal-soal yang berkaitan dengan prisma.
Pada postingan kali ini, kami akan membahas wacana rumus luas permukaan prisma, rumus volume prisma dan pola soal beserta pembahasannya.
Untuk lebih jelasnya silahkan perhatikan prisma segitiga berikut ini beserta jaring-jaringnya!
Dari gambar tersebut di atas, terlihat bahwa prisma segitiga ABC.DEF mempunyai sepasang segitiga yang identik dan tiga buah persegipanjang sebagai sisi tegak. Dengan demikian, luas permukaan prisma segitiga tersebut adalah;
Luas permukaan prisma = luas ΔABC + luas ΔDEF + luas EDAB + luas DFCA + luas FEBC
= 2 x luas ΔABC + luas EDBA + luas DFAC + luas FEBC
= (2 x luas alas) + (luas bidang-bidang tegak)
Jadi, luas permukaan sanggup dinyatakan dengan rumus sebagai berikut.
Pada gambar tersebut di atas, memperlihatkan sebuah balok ABCD.EFGH yang dibagi dua secara melintang. Ternyata, hasil kepingan balok tersebut membentuk prisma segitiga, ibarat pada Gambar (b). Perhatikan prisma segitiga BCD.FGH pada Gambar (c) . Dengan demikian, volume prisma segitiga ialah setengah kali volume balok.
Volume prisma BCD.FGH = ½ × volume balok ABCD.EFGH
= ½ × (p × l × t)
= ( ½ × p × l) × t
= luas bantalan × tinggi
Jadi, volume prisma sanggup dinyatakan dengan rumus sebagai berikut.
1. Perhatikan prisma segitiga pada gambar di bawah ini! Dari gambar tersebut, tentukan:
a. luas bantalan prisma segitiga!
b. volume prisma segitiga!
2. Sebuah prisma mempunyai volume 238 cm3 dan luas bantalan 34 cm2. Tentukan tinggi prisma tersebut!
Jawaban:
Sumber https://www.berpendidikan.com
Pada postingan kali ini, kami akan membahas wacana rumus luas permukaan prisma, rumus volume prisma dan pola soal beserta pembahasannya.
Rumus luas permukaan prisma
Sama ibarat kubus dan balok, asal seruan memilih luas permukaan prisma sanggup dihitung memakai jaring-jaring prisma tersebut. Caranya ialah dengan menjumlahkan semua luas berdiri datar pada jaring-jaring prisma.Untuk lebih jelasnya silahkan perhatikan prisma segitiga berikut ini beserta jaring-jaringnya!
 |
| Gambar: Asal Usul Rumus Luas permukaan prisma |
Dari gambar tersebut di atas, terlihat bahwa prisma segitiga ABC.DEF mempunyai sepasang segitiga yang identik dan tiga buah persegipanjang sebagai sisi tegak. Dengan demikian, luas permukaan prisma segitiga tersebut adalah;
Luas permukaan prisma = luas ΔABC + luas ΔDEF + luas EDAB + luas DFCA + luas FEBC
= 2 x luas ΔABC + luas EDBA + luas DFAC + luas FEBC
= (2 x luas alas) + (luas bidang-bidang tegak)
Jadi, luas permukaan sanggup dinyatakan dengan rumus sebagai berikut.
Luas permukaan prisma = 2 x luas bantalan + luas bidang-bidang tegak
Rumus volume prisma
Untuk lebih memahami asal-usul rumus volume prisma, silahkan perhatikan gambar berikut ini!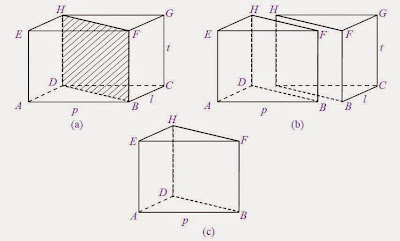 |
| Gambar: Asal seruan rumus volume prisma |
Pada gambar tersebut di atas, memperlihatkan sebuah balok ABCD.EFGH yang dibagi dua secara melintang. Ternyata, hasil kepingan balok tersebut membentuk prisma segitiga, ibarat pada Gambar (b). Perhatikan prisma segitiga BCD.FGH pada Gambar (c) . Dengan demikian, volume prisma segitiga ialah setengah kali volume balok.
Volume prisma BCD.FGH = ½ × volume balok ABCD.EFGH
= ½ × (p × l × t)
= ( ½ × p × l) × t
= luas bantalan × tinggi
Jadi, volume prisma sanggup dinyatakan dengan rumus sebagai berikut.
Volume prisma = luas bantalan × tinggi
Contoh soal dan pembahasannya
Perhatikan pola soal berikut ini!1. Perhatikan prisma segitiga pada gambar di bawah ini! Dari gambar tersebut, tentukan:
a. luas bantalan prisma segitiga!
b. volume prisma segitiga!
2. Sebuah prisma mempunyai volume 238 cm3 dan luas bantalan 34 cm2. Tentukan tinggi prisma tersebut!
Jawaban:
Silahkan Baca juga:
Sumber https://www.berpendidikan.com
loading...
Buat lebih berguna, kongsi:

